The Heckman Curve is Dead. Long live the Heckman Curve!
I recently collaborated on an article on the critical need to support school health in lower and middle-income countries. As one of the examples of the growing momentum for school health, we describe recent studies challenging a long-standing social policy dogma enshrined in what is known as ‘the Heckman Curve’.
The Heckman Curve is an example of a profoundly influential scientific model that is likely wrong and is certainly an oversimplification. The essence of the argument was summarized by the author himself in his original 2006 paper in Science (pg. 1902):
Early interventions targeted towards disadvantaged children have much higher returns than later interventions such as reduced pupil-teacher ratios, public job training, convict rehabilitation programs, tuition subsidies, or expenditures on police.
The Heckman Curve (pictured below from the 2006 paper) shows diminishing returns to investment in terms of future human capital1 for programs aimed to support disadvantaged children as they age. The logic used by Heckman and his proponents is that investing earlier is better: skills beget skills, deficits engender deficits.
The Heckman Curve has been wildly influential in policy making, restricting the vast majority of health investments to children under the age of five. As my colleague and I write in our paper:
Yet to state the obvious, nothing meaningful happens on a child's fifth birthday that demarcates their health status from vulnerable to resilient.
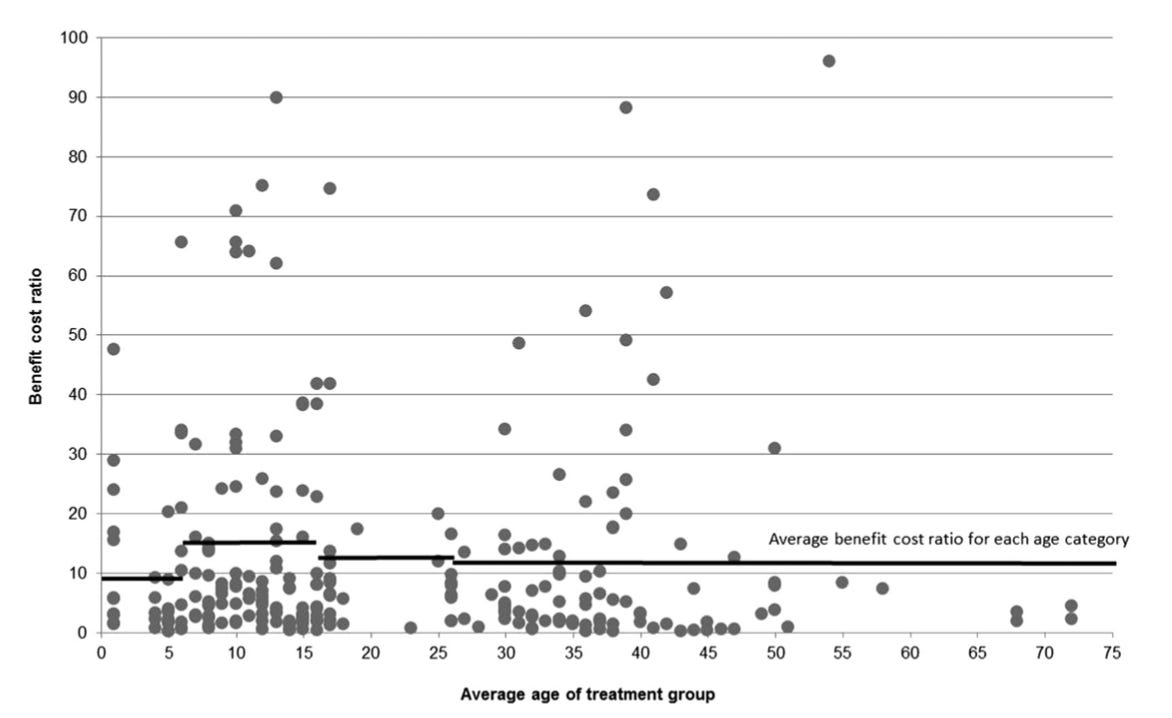
The additional problem with the Heckman Curve is recent research based on more rigorous methods simply have not been able to find any such clear relationship between age of intervention and benefit-cost. The authors of a recent systematic review presented a benefit to cost ratio for each of the programs they examined and there is no clear ‘curve’ in the data that shows a diminished benefit-to-cost ratio as children age (see figure below):
The noise in the relationship between age and benefit cost is perhaps because ‘age of recipient’ is only one potential factor determining the benefit-to-cost ratio. A program targeting young children could be mismanaged (and therefore have a low benefit-to-cost ratio) or, conversely, a program for older adolescents may effectively target those at highest-risk.
Yet the title of this post is The Heckman Curve is Dead. Long live the Heckman Curve! so evidently I don’t see the influence of Heckman's Curve going away any time soon.
I gave the article this title because the logic of the Heckman Curve is so institutionalized in policy frameworks, global organizations and practitioner beliefs, that the Heckman Curve will endure even as its evidence base is called into doubt. Fundamentally, the Heckman Curve will endure because it:
Speaks to our commonsense notions
Is formulated in what appears to be a rigorous mathematical representation that makes the non-specialist hesitant to question it
Addresses a genuine policy need to allocate scarce resources across deserving programs by providing a fundamental criterion
Of course to be clear, I am NOT saying that we should avoid investing in programs for young disadvantaged kids. Only that human development is messy, programs design is complicated, and the notion of a neat curve based on a single variable that explains which programs will be the most cost effective is more fiction than science. Moving to an approach that supports children throughout their development will take more than a few papers challenging the Heckman Curve.
The takeaway is we should be skeptical about such idealized models of development. They are more myth than science.
As someone who is interested in metaphors I have mixed feelings about the phrase ‘human capital’. On the one hand, quantifying the healthy development and safe education of children in terms of their future economic productivity in a globalized world seems to me to be as potentially narrow as valuing a forest only in terms of how its timber can contribute to GDP. The human capital index further reduces this to a single value ranging between 0 and 1. On the other hand, the metric may have value in supporting policy reform and getting other sectors to buy in to educational investments.